Находим уравнения касательных в заданных точках.
х = 2, у(кас) = -1.
х = -2, у(кас) = -8х - 1,
х = 4, у(кас) = 4х - 13.
Находим координаты точек пересечения касательных:
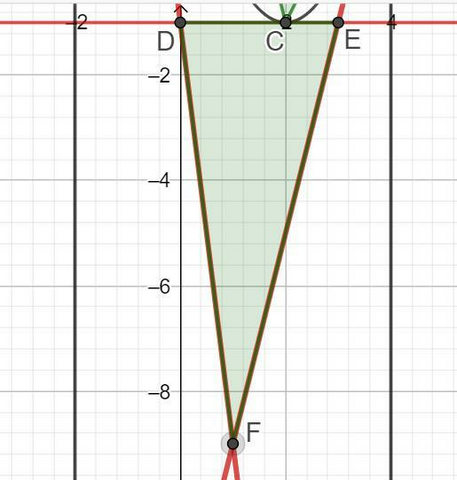
D = (0; -1), E =(3; -1), F = (1; -9).
Пусть точки A(x1; y1), В(x2; y2), С(x3; y3) - вершины треугольника, тогда его площадь выражается формулой:
S = 12x1-x3y1-y3x2-x3y2-y3
В правой части стоит определитель второго порядка. Площадь треугольника всегда положительна.
Дан треугольник с вершинами D(0,-1), E(3,-1), F(1,-9)
Решение. Принимая D за первую вершину, находим:
x1-x3 y1-y3
x2-x3 y2-y3 = 0 - 1-1 - (-9)3 - 1-1 - (-9) =
-1 8 2 8 = -1•8 - 2•8 = -24
По формуле получаем:
S = 12•|-24| = 12
.