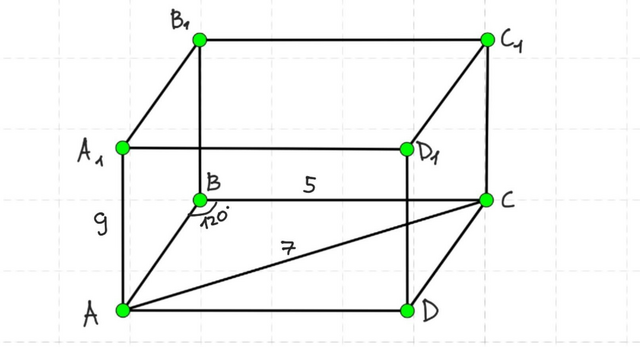
Дано: ABCDA1B1C1D1 — прямоугольный параллелепипед; АА1= 9 см, АС= 7 см, ВС= 5 см, ∠АВС= 120°.
Найти: S боковой поверхности, V(объём)
Решение.
1) У прямого параллелепипеда в основании – параллелограмм, а боковые грани - прямоугольники.
В ΔABC по теореме косинусов найдём сторону АВ.
АС²= АВ²+ВС²–2АВ•ВС•cos120°;
49= AB²+25–2•5•AB•(–½);
49= AB²+5AB+25;
AB²+5AB–24= 0;
По т.Виета решаем это кв.уравнение и получаем: АВ=3 или АВ= –8. Отрицательным не может быть, значит, делаем вывод, что АВ= 3 см.
2) А теперь вспоминаем все формулы (во вложении)
3) Сначала находим площадь основания.
Sосн.= АВ•ВС•sin120°= 3•5• (√3/2)= (15√3)/2.
4) Находим объём:
V= Sосн.•АА1= (15√3)/2 •9= (135√3)/2 (см³).
5) Находим площадь боковой поверхности.
S бок.= 2•АВ•АА1+2•ВС•АА1= 2•3•9+2•5•9= 144 см²
Ответ: S= 144 см², V= (135√3)/2 см³