Образующая усеченного конуса равна 2√3 см, а радиус меньшего основания √3 см. Найдите радиус сферы, описанной вокруг данного усеченного конуса, если угол между его образующей и большим основанием равен 60 °.
Объяснение:
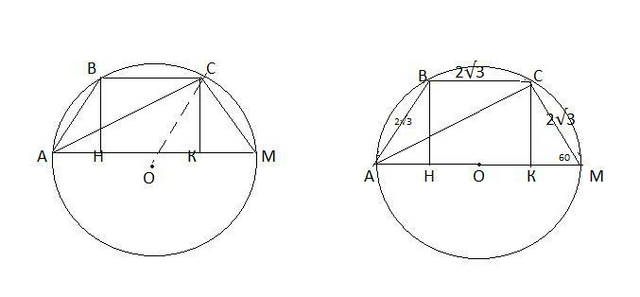
В осевом сечении данной комбинации тел получается равнобедренная трапеция , вписанная в окружность.
АВСМ-равнобедренная трапеция , О-центр описанной окружности., АВ=СМ=2√3, ВС=2√3, ∠СМА=60°. Найти R.
Пусть ВН⊥АМ, СК⊥АМ.Тогда НВСК-прямоугольник, ВС=НК=2√3 см
ΔСКМ прямоугольный. cos60°=КМ/(2√3) , КМ=√3 см ⇒АН=√3см,
sin60°=CК/(2√3) , СК=3 см .
Найдем АК=АН+НК=3√3 (см) и АМ=2√3+2√3=4√3 (см).
ΔАСК-прямоугольный , по т. Пифагора
АС=√ ( (3√3)²+3²)=√36=6 (см)
ΔАСМ , вычислим АМ² , АС²+СМ², затем сравним.
АМ²=(4√3)²=48,
АС²+СМ²=6²+(2√3)²=36+12=48.
Получили АМ²=АС²+СМ² ⇒ ΔАСМ-прямоугольный , по т. обратной т. Пифагора и ∠АСМ=90° ⇒ центр описанной окружности лежит на середине АМ ⇒
R=2√3 cv