Ответ:
№1 (рисунок из условия)
ΔAOB - равнобедренный АО=ОВ (радиусы),
поэтому ∠ВАО = ∠АВО = 30°
∠АОВ = 180 - ∠ВАО - ∠АВО = 120°
Рассмотрим ΔОАС и ΔОВС, они равны по трем сторонам
АС = ВС по свойству двух касательных проведенных из одной
точки. ОС - общая
Как следствие ∠АСО = ∠ВСО
Кроме того ΔОАС и ΔОВС - прямоугольные - радиус перпедикулярен к касательной ∠СОА = ∠СОВ = 1/2 ∠АОВ = 1/2*120° = 60°.
∠ВСО = ∠АСО = 90° - ∠СОА = 90° - 60° = 30°
∠АСВ = ∠АСО + ∠ВСО = 30° + 30° = 60°
Ответ: ∠АСВ = 60°
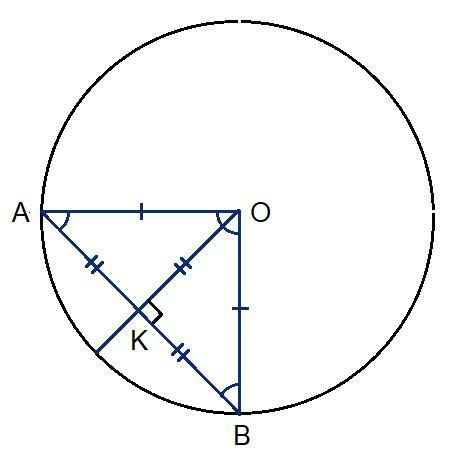
№2 (рисунок Zadacha_0001. точка К = точке С)
Рассмотрим ΔAOB - равнобедренный АО=ОВ (радиусы),
поэтому ∠ВАО = ∠АВО = 45°
∠АОВ = 180 - ∠ВАО - ∠АВО = 90°
ΔAOB - прямоугольный
ОС - высота, а следовательно - медиана ΔAOB,
поэтому СА = СВ = 1/2 AB = 1/2 *26 = 13.
ΔAСО - прямоугольный. ОС⊥АВ.
∠СОА = 90° - 45° = 45°
ΔAСО - равносторонний, ∠СОА =∠САО
поэтому ОС = АС = 13 см
Ответ: ОС = 13 см
№3
а)
1) строим угол равный заданному (базовое построение)
2) откладываем длину одной стороны на одном луче угла
3) откладываем длину другой стороны на втором луче угла
4) соединяем полученные точке
построенный треугольник - искомый
б)
построение бисектрисы угла - базовое
если надо детали - zadacha_0003
Объяснение: