Помогите пожалуйста с заданием.

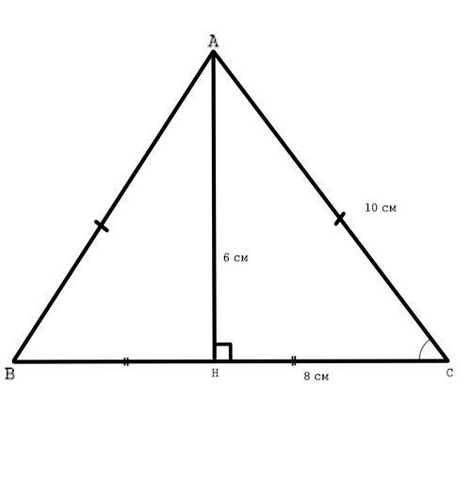
В равнобедренном треугольнике высота, проведённая к основанию - медиана и биссектриса. Следовательно, НС = 16 см:2 = 8 см.

Рассмотрим прямоугольный треугольник АНС. Катеты равны по 6 см и 8 см, значит, АНС - египетский, тогда гипотенуза АС = 10 см (или же можно через теорему Пифагора).

В равнобедренном треугольники углы при основании равны, поэтому не важно какой мы будем брать угол.

Синус - отношение противолежащего катета к гипотенузе.

$sin(ACH) = \frac{AH}{AC} \\sin(ACH) = \frac{6}{10} \\sin(ACH) = 0,6$

Косинус - отношение прилежащего катета к гипотенузе.

$cos(ACH) = \frac{HC}{AC} \\cos(ACH) = \frac{8}{10} \\cos(ACH) = 0,8$

Тангенс - отношение противолежащего катета к прилежащему катету (или же можно его найти через формулу sin(a)/cos(a) = tg(a) ).

$tg(ACH) = \frac{AH}{HC} \\tg(ACH) = \frac{6}{8} \\tg(ACH) =0,75$

Ответ: sin = 0,6; cos = 0,8; tg = 0,75.