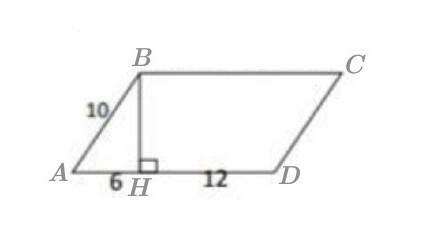
Дано :
Четырёхугольник ABCD — параллелограмм.
ВН — высота.
АВ = 10 (ед).
АН = 6 (ед).
HD = 12 (ед).
Найти :
S(ABCD) = ?
Решение :
- Площадь параллелограмма равна произведению стороны и высоты, опущенной на эту сторону.
То есть —
S(ABCD) = BH*AD
— — —
AD = AH + HD = 6 (ед) + 12 (ед) = 18 (ед).
Рассмотрим ∆АВН — прямоугольный.
По теореме Пифагора —
ВН = √(АВ² - АН²) = √(10² - 6²) = √(100 - 36) = √64 = 8 (ед).
S(ABCD) = BH*AD
S(ABCD) = 8 (ед)*18 (ед)
S(ABCD) = 144 (ед²).
Ответ :
144 (ед²).