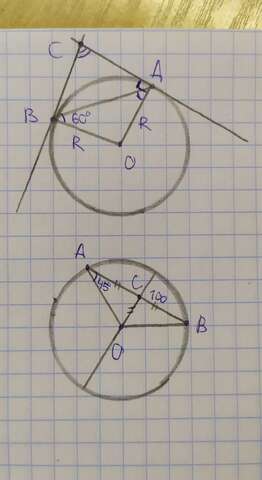
1. Так как стороны ОВ=ОА как радиусы окружности, то треуголньик АВО - равнобедренный, и углы при основании ОВА=ОАВ=60°. Свойство касательной к окружности гласит, что радиус окружности, проведённый в точку касания, перпендикулярен касательной. Значит, углы ОВС и ОАС - прямые, равны 90°. Следовательно, углы АВС=ВАС=90-60=30°. Из суммы углов треугольника АВС находим угол С: 180-30-30=120°.
Ответ: 120°.
2. Проведём диаметр окружности так, чтобы он совпал с опущенным на хорду АВ перпендикуляром. Теорема гласит, что диаметр, перпендикулярный хорде, делит ее на две равные части, т.е. АС=СВ=100:2=50(см). Так как угол ОАС=45° по условию, угол ОСА=90° (тоже по условию), то угол АОС=180-90-45=45°. Следовательно, треугольник АСО - равнобедренный, и АС=ОС=50 см.
Ответ: 50 см.
(Рисунки не совсем точны в плане равнобедренности некоторых треугольников, но на них всё указано).