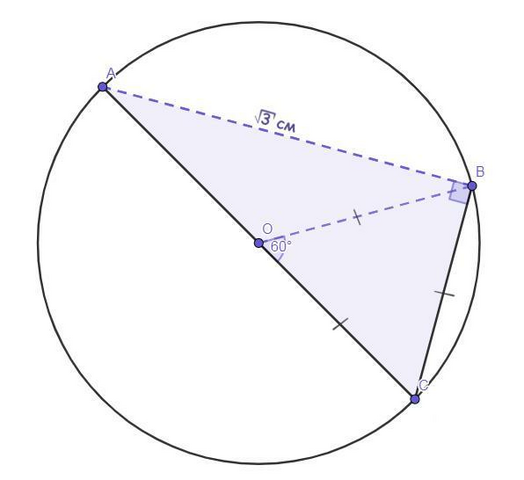
На круге размещены токчи А, В и С так, что АС - диаметр круга, а хорду ВС видно с центра окружности круга под углом в 60°. Найдите радиус круга, если АВ =  см.
см.
- - -
Дано :
Круг.
Точка О - центр данного круга.
Точка А ∈кругу.
Точка В ∈кругу.
Точка С ∈кругу.
АС - диаметр круга.
∠ВОС = 60°.
АВ =  см.
см.
Найти :
ОС = ? (или ОА, это неважно, так как они равны).
Решение :
∠АВС - вписанный (по определению), так ещё и опирается на диаметр АС, следовательно, ∠АВС = 90° (так как диаметр "стягивает" дугу в 180°).
Рассмотрим ΔАВС - прямоугольный.
ОС = ОА (так как радиусы одной окружности). Тогда отрезок ОВ - медиана (по определению), причём проведённая к гипотенузе (АС - гипотенуза, так как лежит против угла в 90°).
- В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна её половине.
Следовательно -
ОВ = ВС = ОС.
Тогда ΔОВС - равносторонний (по определению).
- Каждый угол равностороннего треугольника равен 60°.
Следовательно -
∠ВОС = ∠ОВС = ∠С = 60°.
Тогда -

BC = 1 см.
Ответ :
1 см.