Ответ:
S = √3 ед².
Объяснение:
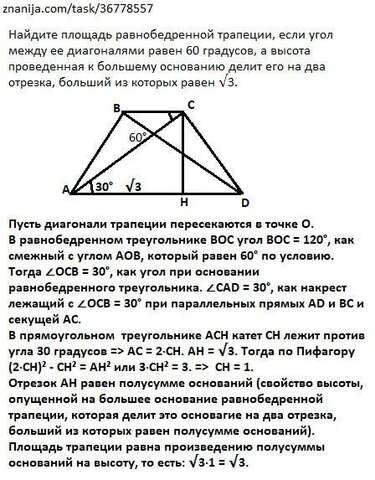
Пусть диагонали трапеции пересекаются в точке О.
В равнобедренном треугольнике ВОС угол ВОС = 120°, как смежный с углом АОВ, который равен 60° по условию. Тогда ∠ОСВ = 30°, как угол при основании равнобедренного треугольника. ∠CAD = 30°, как накрест лежащий с ∠ОСВ = 30° при параллельных прямых AD и ВС и секущей АС.
В прямоугольном треугольнике АСН катет СН лежит против угла 30 градусов => АС = 2·СН. АН = √3. Тогда по Пифагору
(2·СН)² - СН² = АН² или 3·СН² = 3. => СН = 1 ед.
Отрезок АН равен полусумме оснований (свойство высоты, опущенной на большее основание равнобедренной трапеции, которая делит это основание на два отрезка, больший из которых равен полусумме оснований). Итак, полусумма оснований равна √3 (дано). Тогда площадь трапеции равна произведению полусуммы оснований на высоту, то есть: √3·1 = √3 ед².