** стороне AB прямоугольника ABCD как ** диаметре построена окружность ω. Пусть P —...

Question

На стороне AB прямоугольника ABCD как на диаметре построена окружность ω. Пусть P — вторая точка пересечения отрезка AC и окружности ω. Касательная к ω в точке P пересекает отрезок BC в точке Kи проходит через точку D. Найдите AD, если известно, что KD=42 Сроооочнооо помогите,пожалуйста ​

Answer 1

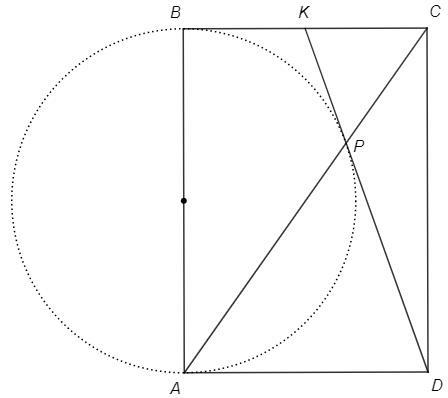
BC, AD - касательные (т.к. перпендикулярны диаметру)

BK=KP, AD=DP (отрезки касательных из одной точки)

△ADP - равнобедренный

△CKP~△ADP (по накрест лежащим при BC||AD)

△CKP - равнобедренный, CK=KP

KP=CK=BK =BC/2 =AD/2

KD =KP+DP =AD/2 +AD =3/2 AD

AD =2/3 KD =42*2/3 =28

---

Comments

почему СК=КР и почему треугольник СКР?

---

Треугольники ADP и CKP подобны. ADP равнобедренный, следовательно CKP тоже равнобедренный.

---

спасибо

---

А как вам такое? :) Очевидно (сравнением углов), что KO II CA ... или даже еще проще :) BP перпендикулярно AC => треугольник BPC прямоугольный => BK = KP = KC = AD/2 => AD = DP = (2/3)KD. Забавно :) на ютубе часто такие задачки выкладывают в качестве "вирусных". Чаще всего они очень простые, "одноходовки".

---

То, что KO II CA, сразу дает BK = KC; O - конечно, центр окружности.

---

Вот наиболее красивое и понятное решение этой простенькой задачки :) Точки касания B и P симметричны относительно KO. => Равны углы CAB и KOB; (оба равны половине центрального угла POB) => KO II CA; Дальше BO = AO => BK = KС= (тут уже все решено, дальше уже чистая схоластика) = KР = BC/2 = AD/2 => AD = DP = (2/3)KD; Вот. Это - то, что надо :)