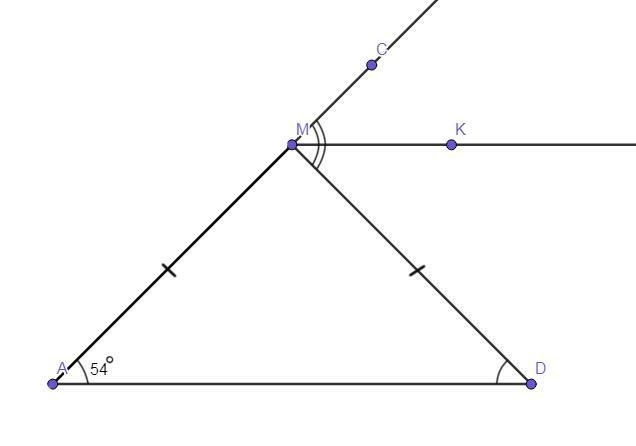
Чертёж смотрите во вложении.
Дано:
ΔAMD.
∠CMD - внешний.
МК - биссектриса ∠CMD.
МК║AD.
∠MAD = 54°.
Найти:
∠AMD = ?
Решение:
Так как биссектриса МК внешнего угла ∠CMD параллельна стороне AD ΔAMD, то ΔAMD - равнобедренный (по признаку равнобедренного треугольника). Причём AD - его основание.
∠MAD = ∠ADM = 54° (так как они у основания в равнобедренном треугольнике). Тогда, по теореме о сумме углов треугольника, ∠AMD = 180°-∠MAD-∠ADM = 180°-54°-54° = 72°.
Ответ: 72°.