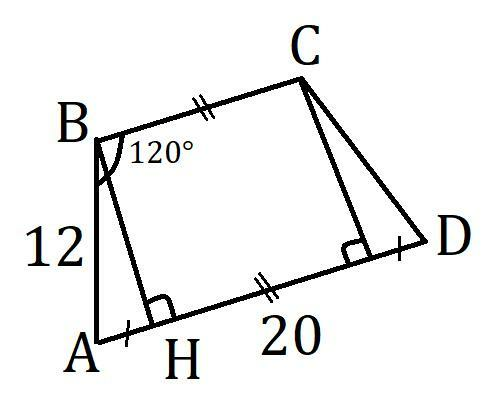
В трапеции ABCD:
AB=CD=12, AD=20, ∠ABC=120°.
Проведём высоту трапеции BH. Тогда ΔBHC - прямоугольный и ∠ABH=120°-90°=30°
Катет лежащий напротив угла в 30° вдвое меньше гипотенузы, откуда AH=AB:2=12:2=6
BC=20-2·AH=20-12=8
Осталось найти высоту трапеции.
В том же прямоугольном ΔBHC: AB=12, AH=6, по теореме Пифагора
BH² = AB²-AH² = 12²-6² = (12-6)(12+6) = 6·18 = 36·3
BH = 6√3

Ответ: 84√3.