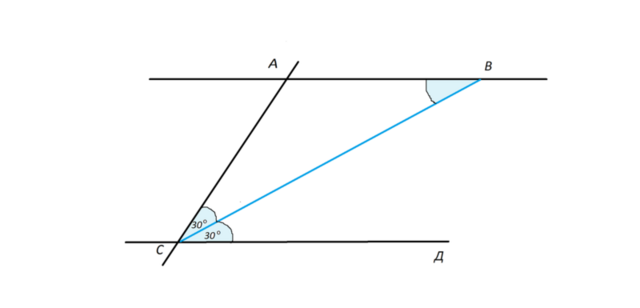
Если я правильно поняла условие, рисунок должен выглядеть несколько иначе..
АВ параллелльна СД. Угол АСД=60, СВ - биссектриса угла С. Найти углы треугольника АСВ.
По условию АВ параллельна СД. Нарисуем эти прямые.
Из С проведем секущую к АВ под углом 60° к СД.
Получившийся ∠С разделим биссектрисой СВ на 2 равных.
Получился треугольник АСВ, в котором ∠АВС = ∠ВСД как накрестлежащие.
А так как ∠ВСД =∠АСВ ( угол С делится биссектрисой СВ пополам),
то углы треугольника АВС при основании СВ равны половине угла С. т.е по 30°. Оставшийся угол при вершине А треугольника САВ найти из суммы углов треугольника не составит труда:
∠ САВ=180°-(АСВ+АВС)=120°
Ответ: 30°,120°,30°