Ответ:
26.8
Объяснение:
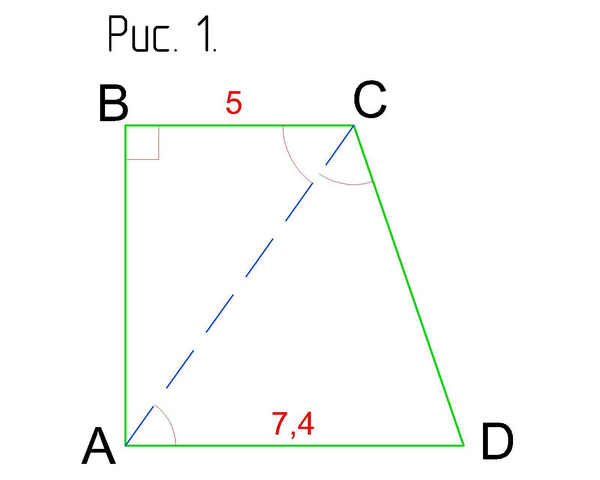
Выполним рисунок. (см. Рис. 1)
Прямоугольная трапеция ABCD, меньшее основание BC=5, большее основание DA=7.4, AC -биссектриса ∠С, AB⊥BC, AB⊥DA, DA║BC.
∠ACD=∠ВСА т.к. АС- биссектриса,
∠DAC=∠ВСА, как накрест лежащие, значит ∠ACD=∠DAC=∠ВСА.
ΔACD-равнобедренный, т.к. ∠ACD=∠DAC. Тогда AD=CD=7.4.
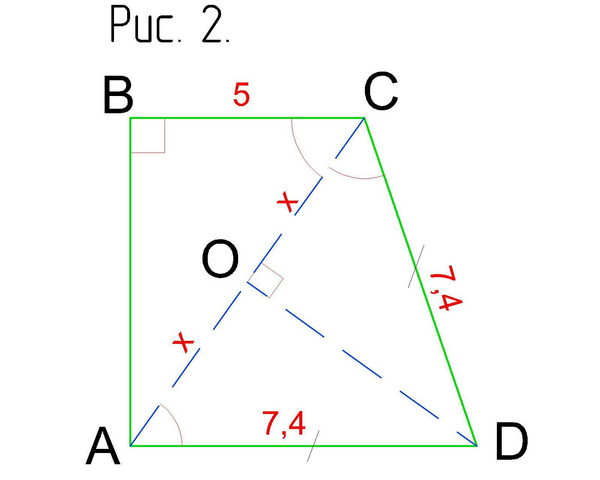
Выполним дополнительное построение (см. Рис. 2). Проведем высоту DO в ΔACD. Т.к. ΔACD-равнобедренный, то DO также является медианой, значит, AO=OC.
Пусть АО=х, тогда АС=2х.
ΔАВС ~ ΔDAO по двум углам ∠DAC=∠ВСА и ∠АВС=∠AOD=90°.
Тогда 
Из прямоугольного ΔАВС найдем катет АВ:
 .
.
Значит в трапеции ABCD: AB=7, BC=5, CD=7.4, DA=7.4.