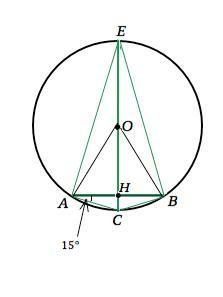
Дан круг, радиус ОС которого перпендикулярен к хорде АВ. Найдите угол АОВ, если угол ВАС = 15 градусов.
—————
Ответ: 60°
Объяснение:
Сделаем рисунок, соответсвующий условию задачи, и дополним его, соединив концы диаметра с концами хорды АВ. ЕС - диаметр. Радиус ОС перпендикулярен хорде (дано) и при пересечении в т.Н делит ее пополам (свойство). Тогда ∆ АНС=∆ ВНС по двум катетам. =>
∠АВС=∠ВАС=15°
Из суммы углов треугольника ∠АСВ=180°-2•15°=150°
Четырехугольник АСВЕ вписанный. Сумма противоположных углов вписанного четырехугольника 180°, поэтому вписанный ∠АЕВ=180°-150°=30°.
Центральный угол вдвое больше вписанного угла (свойство) . ∠АОВ=2•30°=60°