Ответ:
1-ая задача:
вкратце)
расстояние- это перпендикуляр
поэтому треугольник АВН прямоугольный.(Н- точка расстояния от М до АВ)
угол САМ равен МАН(т.к. АМ бисс)
АМ- общая сторона
из этого АСМ=АМН(треугольники)
из чего СМ=МН=7см
ответ:7см
2-ая задача:
Любая точка биссектрисы неразвёрнутого угла равноудалена от сторон этого угла.
Доказательство:
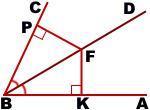
Рассмотрим треугольники BFK и BFP.
∠BKF=∠BPF=90º, ∠KBF=∠PBF (так как по условию BD — биссектриса ∠ABC).
BF — общая сторона.
Значит, ∆BFK=∆BFP (по гипотенузе и острому углу).
Из равенства треугольников следует равенство соответствующих сторон: FK=FP.
Что и требовалось доказать.