рівнобічна трапеція MNKF описана навколо кола Знайти плозу трапеції , якщо оснлви NK і MF...

Question

Дан 1 ответ

Правильный ответ

Ответ:

Площа трапеції дорівнює 32√3 см²

Объяснение:

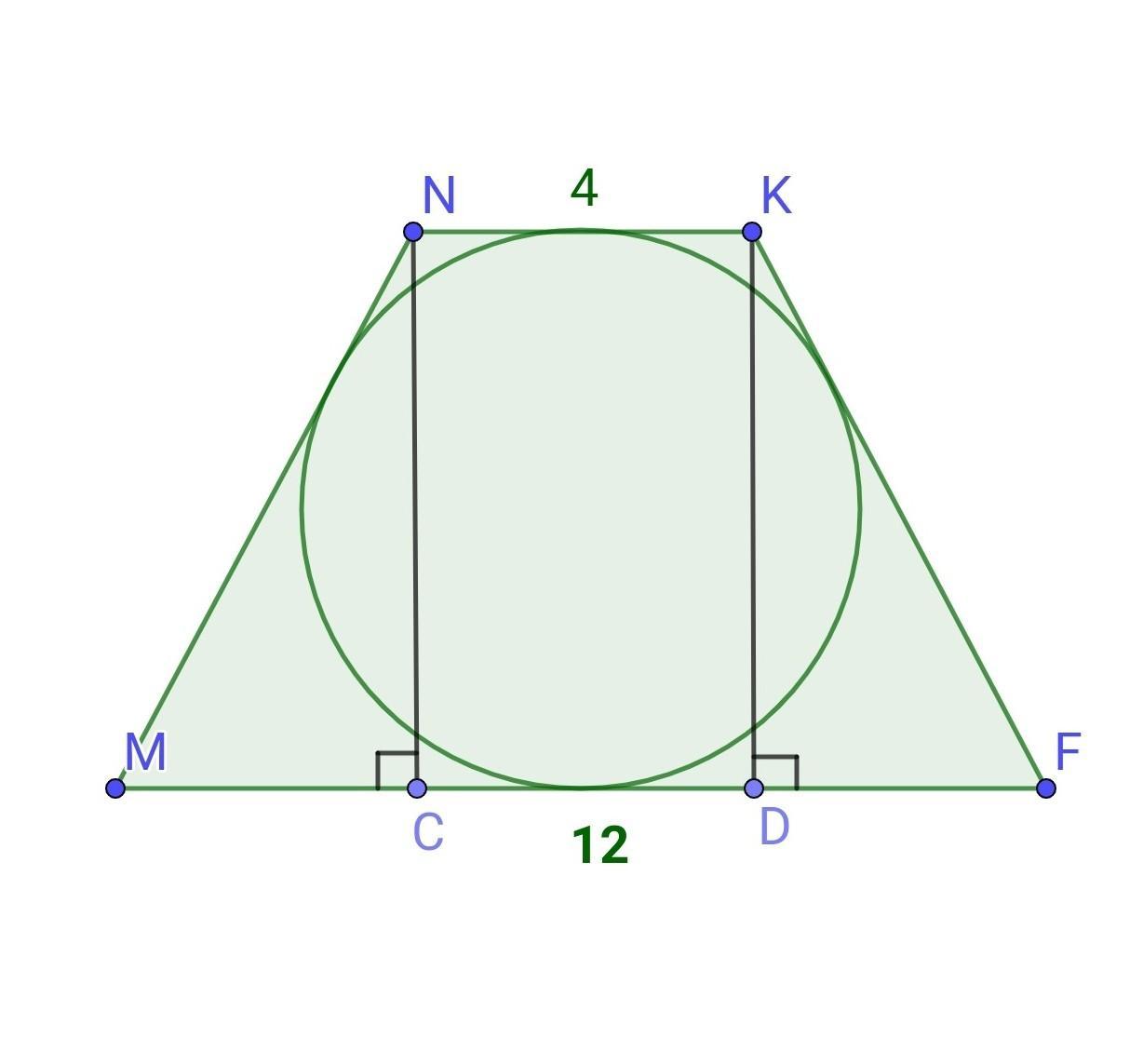
Рівнобічна трапеція MNKF описана навколо кола. Знайти площу трапеції , якщо основи NK і MF відповідно дорівнюють 4 см і 12 см.

Нехай маємо рівнобічну трапецію MNKF, NK||MF, MN=KF, NK = 4 см, MF= 12 см.

1) Оскільки у рівнобічну трапецію вписане коло, то суми ії протилежних сторін рівні (властивість чотирикутника, описаного навколо кола), тобто:

MN+KF=NK+MF.

Звідси:

2MN=4+12=16, MN=KF=16:2= 8 (см)

2) Проведемо дві висоти NC і KD. Тоді △MNC =△FKD за гіпотенузою і гострим кутом (∠M=∠F -як кути при основі рівнобічної трапеції, MN=KF - як бічні сторони рівнобічної трапеції).

Тому MC=DF.

3) Оскільки NKDC - прямокутник, то CD=NK=4 (см). Маємо:

$MC = DF = \dfrac{MF - NK}{2} = \dfrac{12 - 4}{2} = 4$ (см)

4) У прямокутному трикутнику MNC (∠MCN=90°) за теоремою Піфагора знайдемо катет NC:

$NC = \sqrt{ {MN}^{2} - {MC}^{2} } = \sqrt{ {8}^{2} - {4}^{2} } = \sqrt{48} = \bf 4 \sqrt{3}$ (см)

5) Знайдемо площу трапеції:

$S_{MNKF} = \dfrac{NK + MF}{2} \times NC = \dfrac{4 + 12}{2} \times 4 \sqrt{3} = \bf32 \sqrt{3}$ (см²)

Відповідь: 32√3 см²

Якщо знати теорему: висота рівнобічної трапеції, в яку можна вписати коло, є середнім геометричним ії основ, то маємо:

$\bf NC = \sqrt{NK \times MF} = \sqrt{4 \times 12} = \sqrt{48} = 4 \sqrt{3}$ (см)

Отже, задачу можна вирішити за дві дії.

#SPJ1

ReMiDa_zn (1.2k баллов) 14 Дек, 23