Дві сторони трикутника дорівнюють 3 см і 5 см, а відношення радіуса кола, описаного...

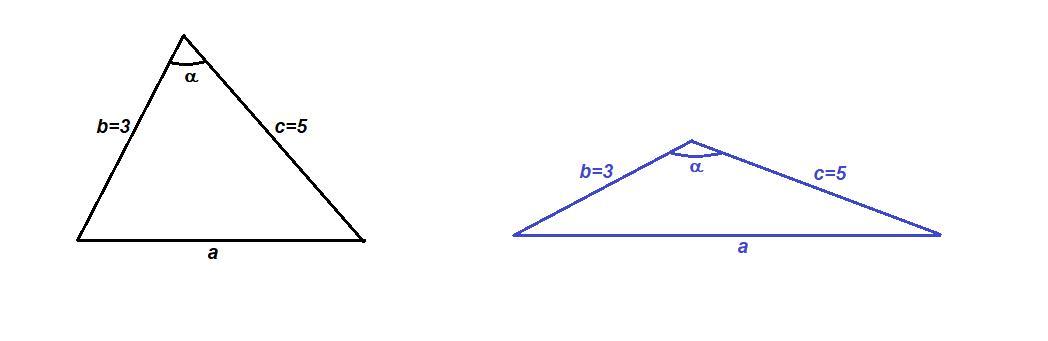
Ответ:

√19 cм или 7 см

Задача имеет два решения.

Объяснение:

По следствию из теоремы синусов, отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу описанной окружности:

$2R=\dfrac{a}{\sin\alpha }$ ⇒ $\sin\alpha =\dfrac{a}{2R}$

По условию:

$\dfrac{R}{a}=\dfrac{1}{\sqrt{3}}$ ⇒ $a=R\sqrt{3}$ .

$\sin\alpha =\dfrac{R\sqrt{3}}{2R}=\dfrac{\sqrt{3}}{2}$

Учитывая, что

$\sin\alpha =\sin(180^\circ -\alpha )$ ,

$\alpha=60^\circ$ или $\alpha=120^\circ$

1) $\alpha=60^\circ$

$\cos60^\circ =\dfrac{1}{2}$

По теореме косинусов:

$a^2=b^2+c^2-2bc\cdot \cos\alpha$

$a^2=9+25-2\cdot 3\cdot 5\cdot \dfrac{1}{2}=34-15=19$

$\boldsymbol{a=\sqrt{19}}$ см

2) $\alpha=120^\circ$

$cos120^\circ =-\dfrac{1}{2}$

По теореме косинусов:

$a^2=b^2+c^2-2bc\cdot \cos\alpha$

$a^2=9+25-2\cdot 3\cdot 5\cdot \left(-\dfrac{1}{2}\right)=34+15=49$

a = 7 см