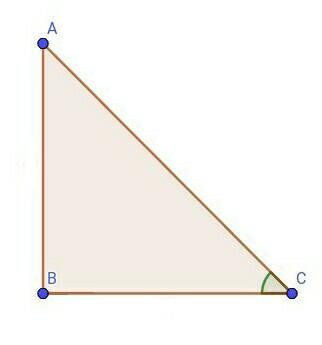
Дано:
△ABC - прямоугольный;
∠С = 60˚;
ВС (катет) + AС (гипотенуза) = 15 см.
Найти:
∠А = ?˚; ВС = ? см (катет).
Решение:
Сумма острых углов в прямоугольном треугольнике равна 90°.
=> ∠А = 90˚ - 60˚ = 30˚.
Катет, лежащий напротив угла в 30°, равен половины гипотенузы.
=> ВС = АC * 1/2.
Пусть x см равен гипотенуза, тогда катет равна 1/2x см. Их сумма равна 15 см.
Составим и решим уравнение:
x + 1/2x = 15
3/2x = 15
x = 15 : 3/2
x = 15/1 * 2/3
x = 10
10 см равна гипотенуза АС => катет ВС будет равен 5 см.
Можно проверить по т.Пифагора, является ли катет ВС наименьшим.
AB = √(10² - 5²) = √(100 - 25) = √75 = 5√3 → 5√3 > 5 => BC - наименьший катет.
Ответ: ∠A = 30˚; BC = 5 см.