Задача#1.
Дано:
∠АВС - ? в 8 раз > ∠CBD.
Найти:
∠АВС - ?
Решение:
Пусть х° - ∠CBD, тогда 8х° - ∠АВС
Сумма смежных углов равна 180°
х + 8х = 180
9х = 180
х = 20
20° - ∠CBD
∠ABC = 20˚ * 8 = 160˚
Ответ: 160°
Задача#2
Дано:
АВ ⊥ CD
∠EOD = 60˚
Найти:
∠СОЕ - ?
Решение:
Перпендикулярные прямые - две прямые, которые образуют 4 прямых угла.
АВ и CD - перпендикулярные прямые, по условию.
=> ∠АОЕ = 90° - 60° = 30°
Так как ∠СОА = 90° => ∠СОЕ = З0° + 90° = 120°
Ответ: 120°
Задача#3
Решение:
1) неверно, так как такой теоремы не существует.
2) неверно, так как такой теоремы не существует.
3) неверно, так как такой теоремы не существует.
4) верно, это 2 признак равенства треугольников.
Ответ: 4)
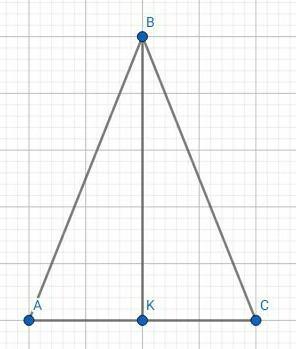
Задача#4
Дано:
△АВС
ВК - биссектриса
∠А = 28°
∠АВК = 30°
Найти:
∠С - ?
Решение:
Так как BK - биссектриса => ∠АВС = 30° * 2 = 60°, так как биссектриса делит угол на 2 равных угла.
Сумма углов треугольника равна 180°
=> ∠С = 180° - (60° + 28°) = 92°
Ответ: 92°
Задача#5
Дано:
Треугольник АВС - равнобедренный
∠А = 35°
Найти:
∠В - ?
Решение:
Так как △АВС - равнобедренный => ∠А = ∠С, по свойству равнобедренного треугольника.
Сумма углов треугольника равна 180°.
=> ∠В = 180˚ - (35˚ + 35˚) = 110˚
Ответ: 110°
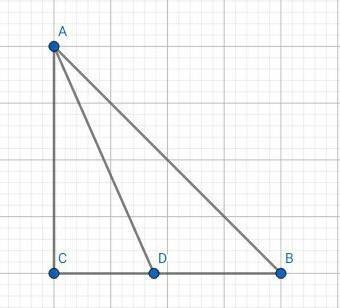
Задача#6
Дано:
△АВС - прямоугольный.
∠С = 90°
AD - биссектриса ∠A
∠ADC = 75˚
АВ = 16 см
Найти:
а) ∠А и ∠В - ?
б) ВС - ?
Решение:
а) Сумма острых углов прямоугольного треугольника равна 90°
=> ∠CAD = 90˚ - 75˚ = 15˚
Так как AD - биссектриса => ∠А = 15° * 2 = 30°, так как биссектриса делит угол на 2 равных угла.
Сумма острых углов прямоугольного треугольника равна 90°
=> ∠В = 90° - 30° = 60°
Ответ: 30°, 60°.
б) Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы.
∠А = 30°, из а) => ВС = 16/2 = 8 см
Ответ: 8 см
Рисунки 4 и 6 задачи.