плоскости двух сечений цилиндра проходящих через одну образующую. Найдите площадь боковой...

Ответ: S(бок) = $\frac{30\pi \sqrt{7} }{4}$ см²

Объяснение:

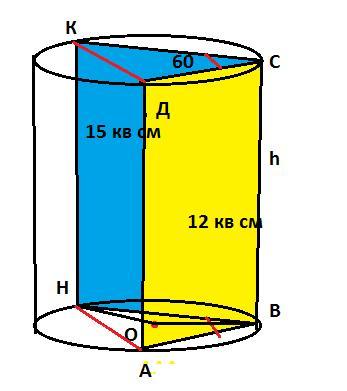
Обозначим высоту цилиндра (образующую) как h

Тогда S(НВСК_=НВ*h (1)

а S(ABCD) = AB*h (2). Разделим одно уравнение на другое и получим,

$\frac{HB}{AB} = \frac{15}{12} = \frac{5}{4}$ Значит НВ = $\frac{5}{4}$ АВ

Тогда по теореме косинусов из треугольника НАВ

НА² = АВ²+НВ²-2*АВ*НВ*cos60°

НА²= $\frac{25}{16}$ НВ² +НВ²-2* $\frac{5}{4}$ *НВ²*cos60°

НА²= $\frac{21}{16}$ НВ Отсюда НА= $\frac{\sqrt{21}}{4}$ НВ

По теореме синусов

$\frac{HA}{2sin60} = r$

Значит r= $\frac{\sqrt{7} }{4}$ НВ

Тогда S(бок) = 2πrh = 2π $\frac{\sqrt{7} }{4}$ НВ*h но НВ*h=15 см²

S(бок) = $\frac{30\pi\sqrt{7} }{4}$ см²