Ответ:
∠АОВ=36°
Объяснение:
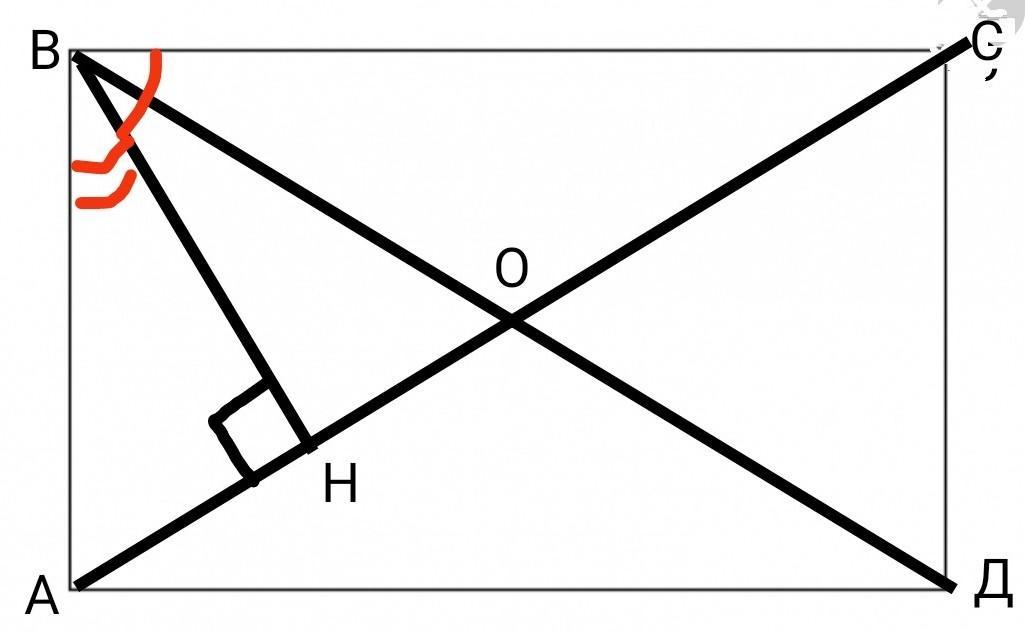
ДАНО:
прямоугольник АВСД, АС и ВД – диагонали прямоугольника; т. О – точка пересечения диагоналей; ВН – высота, проведенная к диагонали АС
НАЙТИ: ∠АОВ
РЕШЕНИЕ : обозначим пропорции 4 : 1, как 4х и х. Так как угол В=90°, составим уравнение:
4х+х=90
5х=90
х=90÷5
х=18; ∠АВН=18°
∠НВС= 4×18=72°;
Рассмотрим ∆ АВН. Он прямоугольный и так как сумма острых углов прямоугольного треугольника составляет 90°, то ∠ВАН=90–∠АВН=90–18=72°
∠НАВ в ∆АВН и ∠ОАВ в ∆АВО – это один и тот же угол равный 72°.
Диагонали прямоугольника равны и точкой пересечения делятся пополам, поэтому ∆АВО – равнобедренный → АО=ВО → ∠ВАО=∠АВО=72°.
Из ∆АВО: сумма углов треугольника равна 180°, тогда ∠АОВ=180–∠АВО–∠ВАО=
=180–72–72=180–144=36°
∠АОВ=36°