Ответ:
Довели, що бісектриси двох кутів, прилеглих до однієї сторони паралелограма взаємно перпендикулярні.
Объяснение:
Доведіть що бісектриси двох кутів прилеглих до однієї сторони паралелограма взаємно перпендикулярні.
Доведення
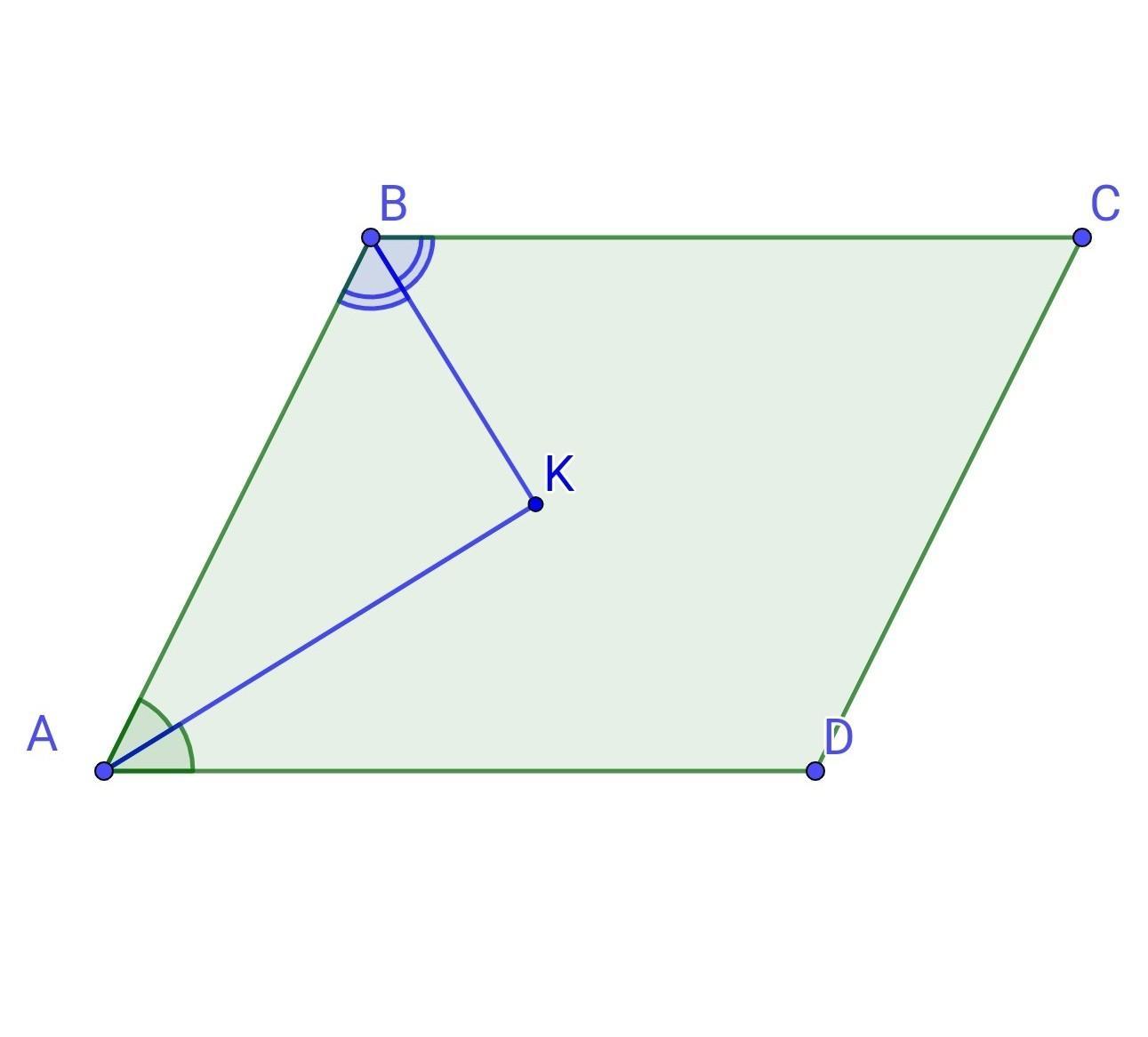
Нехай ABCD - даний паралелограм, ВК і АК - бісектриси кутів В і А відповідно.
1.
Так як сума сусідніх кутів паралелограма дорівнює 180° (за властивістю), то:
∠А + ∠В = 180°.
2.
ВК - бісектриса кута В, отже ∠АВК = ½ • ∠В.
АК - бісектриса кута А, отже ∠ВАК = ½ • ∠А.
3.
Розглянемо △АВК.
За теоремою про суму кутів трикутника маємо:
∠ВАК + ∠АВК + ∠К = 180°
Тоді:
∠К = 180° - (∠ВАК + ∠АВК) = 180° - (½ • ∠А + ½ • ∠В) =
= 180 -½ • (∠А + ∠В) = 180° - ½ • 180° = 180° -90° = 90°.
Отже AK⟂BK, що і треба довести.
#SPJ1