У равнобедренного треугольника ABC (AB = BC) , угол B = 80 градусов, BD = медиана....

Question

У равнобедренного треугольника ABC (AB = BC) , угол B = 80 градусов, BD = медиана. Найдите все углы треугольника ABD.

Answer 1

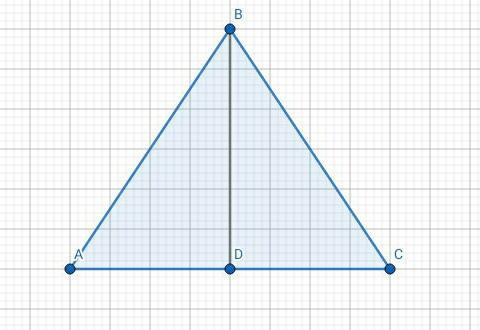
Дано:

равнобедренный △АВС.

АВ = ВС

∠В = 80°

BD - медиана.

Найти:

∠ABD, ∠BAD, ∠ADB.

Решение:

Так как △АВС - равнобедренный => BD - медиана, высота, биссектриса.

Так как BD - биссектриса => ∠ABD = ∠CBD = 80˚/2 = 40˚

△АВС - равнобедренный => ∠А (он же BAD) = ∠С

Сумма углов треугольника равна 180°.

=> 180° - 80° = 100˚ - сумма ∠С и ∠А (BAD)

∠А (BAD) = ∠С = 100°/2 = 50°

Сумма углов треугольника равна 180°.

Так как BD - высота => ∠ADB = 90˚

Ответ: 40°, 50°, 90°.

---

Answer 2

Ответ:

1.∠A=∠C= (180°-80°)/2 =50°

2.∠ABM=∠CBM=80°/2=40°

3.∠AMB=∠CMB=90°

Объяснение:

1. По свойству равнобедренного треугольника углы при основании равны. Зная что сумма углов треугольника =180 получаем 80+2х=180, откуда х=50° т.е. ∠BAM=∠BCM= (180°-80°)/2 =50°

2. Рассмотрим получившиеся треугольники AMB и CMB:

AB=BC(условие), AM=MC(BM-медиана), ∠BAM=∠BCM

следовательно ΔAMB = ΔCMB(1-й признак равенства треугольников).

3. ∠ABM=∠CBM=80°/2=40°

∠AMB=∠CMB=180°/2=90°