В треугольнике ABC BC=34 см. Из середины отрезка BC к прямой АС проведен перпендикуляр,...

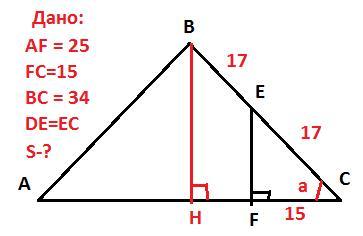
Ответ: S = 320 см²

Объяснение:

Из прямоугольного треугольника CFE найдем косинус угла С

cos a = $\frac{15}{17}$ , но он нам вовсе не нужен, зная его мы найдем синус этого угла: sin a = $\sqrt{1-cos^2a} = \sqrt{1 -\frac{(15)^2}{(17)^2}$ = $\frac{8}{17}$

Теперь отношение ВН/ВС = sina Отсюда

ВН = ВС*sina = $\frac{8}{17} *34$ = 16 см

Тогда S = 0,5*AC*BH = 0,5*40*16= 320 см²