Точка касания вписанной в равнобедренный треугольник окружности делит его боковую сторону...

Question

Точка касания вписанной в равнобедренный треугольник окружности делит его боковую сторону на отрезки разность которых равна 2см (больший отрезок прилегает к углу, противолежащему основанию) Найдите стороны этого треугольника, если его периметр равен 28см. Решите задачу с помощью уравнения, объясните решение и запишите ответ.

Answer 1

Ответ:

Боковые стороны равны 10 см, основание равно 8 см.

Объяснение:

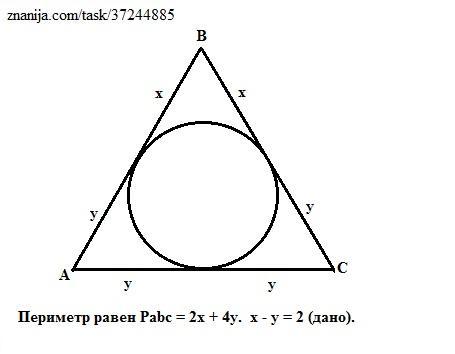
Дан равнобедренный  треугольник АВС с основанием АС. По условию точка касания делит боковые сторону  (они равны) на отрезки x и y, считая от вершины В.

Касательные к вписанной окружности , проведенные из одной вершины, равны. Следовательно, периметр треугольника равен:

Рabc = 2x +4y = 28 см. (1)  (уравнение)

x - y =2 (дано)  => y = x-2. Подставляем это значение в (1):

2x + 4x - 8 = 28  => x = 6 см.   y = 4 см.  =>

Боковые стороны равны x+y = 10 см, основание равно 2y = 8 см.

---

Comments

очень плохо