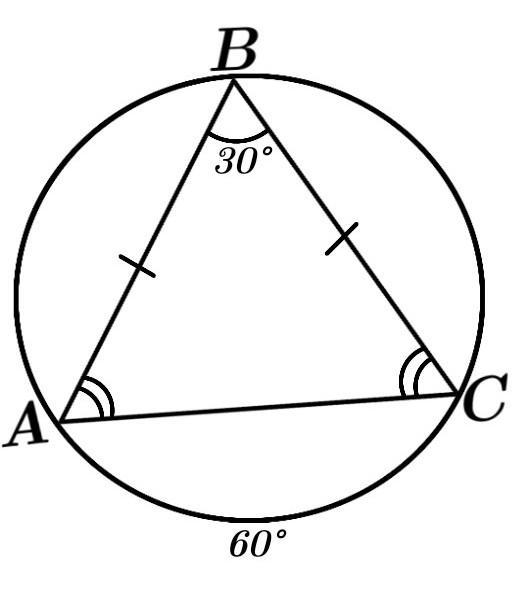
Дано :
∆АВС — равнобедренный, вписан в окружность.
АС — основание = радиус описанной окружности.
Найти :
∪АС = ?
∪АВ = ?
∪ВС = ?
Решение :
- Если хорда равна радиусу окружности, то она стягивает дугу в 60°.
АС — хорда описанной окружности, поэтому ∪АС = 60° (по выше сказанному).
∠АВС — вписанный (по определению).
По свойству вписанных углов —
∠АВС = 0,5*∪АС
∠АВС = 0,5*60°
∠АВС = 30°.
- Углы у основания равнобедренного треугольника равны.
Поэтому, по теореме о сумме углов треугольника —
∠АСВ = ∠ВАС = 0,5*(180° - ∠АВС) = 0,5*(180° - 30°) = 0,5*150° = 75°.
Причём ∠АСВ и ∠ВАС — вписанные по определению.
- Равные вписанные углы опираются на равные дуги.
Тогда —
∪АВ = ∪ВС = 2*∠ВАС = 2*75° = 150°.
Ответ :
60°, 150°, 150°.