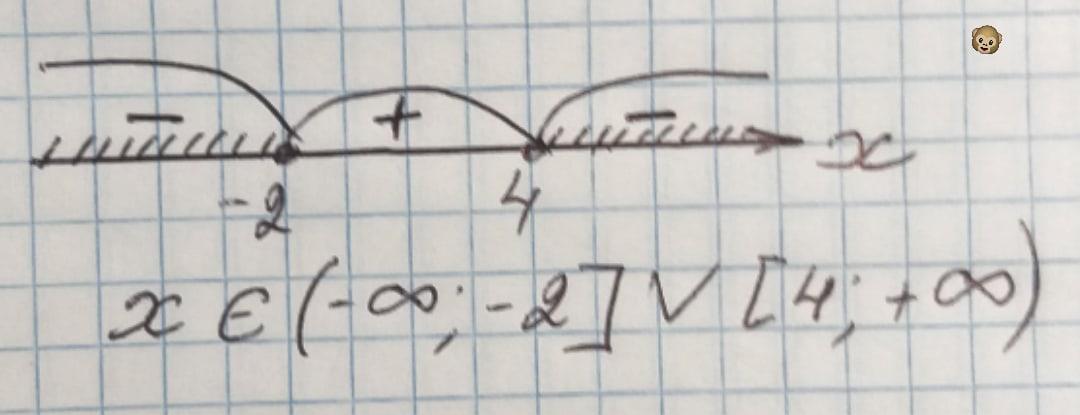Ответ и с пояснениям

Ответ:

x ∈ (-∞ ; -2]∪[4 ; +∞)

Пошаговое объяснение:

$8 + 2x-x^2\leq 0\\$

Для решения этого неравенства нужно найти его корни. Для этого приравняем его к 0 и решим:

$8 + 2x-x^2=0\\D = 2^2-4*8*(-1)=36\\x_1=\frac{-2+\sqrt{36} }{2*(-1)}= -2\\x_2=\frac{-2-\sqrt{36} }{2*(-1)}= 4$

Теперь полученные корни наносим на координатную прямую. Расставляем знаки функции на интервалах (подставляем любые числа на этих интервалах и проверяем знак функции). И выбираем те интервалы, которые отрицательные (т.к. функция ≤ 0).

Ответ и с пояснениям​

Ответ и с пояснениям