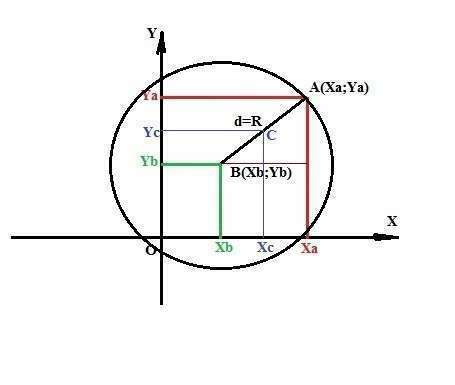
1. Для любых двух точек на плоскости с координатами А(Хa;Ya) и В(Хb;Yb) квадрат расстояния между ними по Пифагору равен: d²=(Xa-Xb)²+(Ya-Yb)².
Для окружности с центром в точке В по определению это расстояние одинаково для ЛЮБОЙ точки А и равно R.
Таким образом, R²=(X-Xb)²+(Y-Yb)².
2. Пусть точка С - середина отрезка АВ.
Тогда модули разности координат равны, то есть
|Xc-Xb|=|Xa-Xc| (1) и |Xa-Xc|=|Ya-Yc| (2).
Из (1) имеем: а) Xc-Xb=Xa-Xc => 2Xc=Xa+Xb и Xc=(Xa+Xb)/2.
б) Xс-Xb=-(Xa-Xc) => Xb=Xa, что невозможно.
Точно так же и для (2).
Значит C((Xa+Xb)/2;(Ya+Yb)/2).
В нашем случае:
А(-3;4) и В(3;-6). Тогда С((-3+3)/2;(4+(-6)/2)) или С(0;-1).
Ответ: С(0;-1).