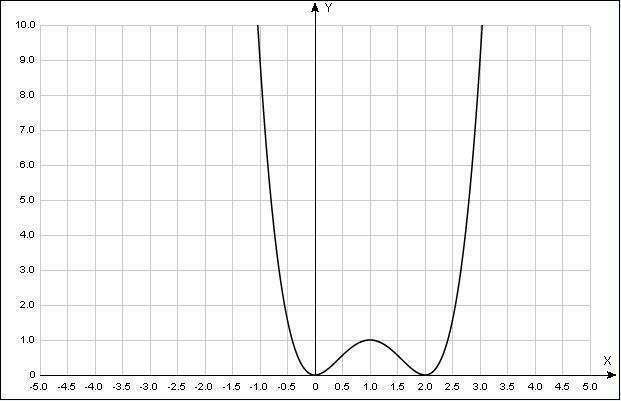
F(x) = x^2*(x^2 - 4x + 4) = x^4 - 4x^3 + 4x^2
1) Область определения функции (ОДЗ): вся числовая ось (любые х)
2) Область значений функции: y≥0
3) Функция не является ни четной, ни нечетной, т.к. f(x) ≠ f(-x) и f(x)≠ -f(x)
4) Функция непрерывная, т.к. ОДЗ - вся числовая ось.
5) Нули функции: x^2*(x - 2)^2 = 0, x=0, x=2, т.е. (0:0) и (2;0). Функция пересекает ось Оу в точке: (0;0).
6) f '(x) = 4x^3 - 12x^2 + 8x = 0
x^3 - 3x^2 + 2x = 0, x*(x^2 - 3x + 2) = 0
x1 = 0, x2 = 2, x3 = 1
Производная отрицательна при: х∈(-бесконечность; 0)u(1;2), функция убывает
Производная положительна при: х∈(0;1)u(2;+бесконечность), функция возрастает.
x=0 и x=2 - точки минимума
x=1 - точка изгиба (выпуклость функции)
7) График строится исходя из полученных сведений пп.1)-6), и с добавлением произвольных точек (значение высчитать вручную, устно). График прикреплен.