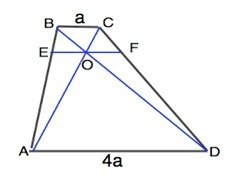
Обозначим трапецию АВСD. Пусть ВС=а, тогда АD=4а.
1) Треугольники, образованные пересекающимися диагоналями и основаниями трапеции, подобны по равным углам: вертикальные при точке пересечения О и накрестлежащие при основаниях, и k=AD:ВС=4:1⇒
АО:СО=4:1
2) Так как ЕF параллельна основаниям трапеции, ∆АВС и ∆АЕО подобны с коэффициентом подобия АО:АС,=4:(4+)=4/5
Аналогично из подобия ∆ ОDF и BDC отношение ОD:ВD=4/5
Тогда ЕО:ВС=ОF:ВС=4/5, откуда ЕО=ОF=8:2=4
Из отношения ЕО:ВС=4/5 находим ВС=5 (ед. длины)
АD=4ВС=4•5=20 (ед. длины)
———
Полезно запомнить это свойство трапеции:
Отрезок, параллельный основаниям трапеции, проходящий через точку пересечения диагоналей и соединяющий две точки на боковых сторонах,делится точкой пересечения диагоналей пополам.