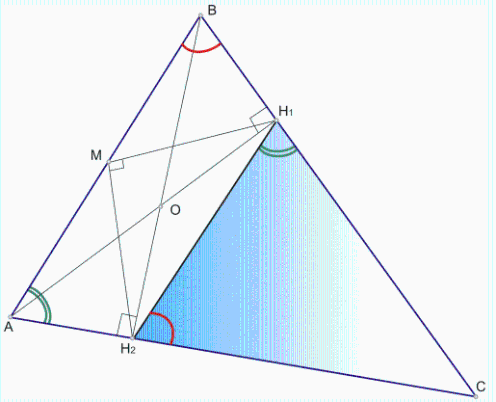
М - центр описанной вокруг четырехугольника ABH1H2 окружности (угол AH2B = угол AH1B = 90), тогда
треугольник MH1H2 - равнобедренный и угол MH1H2 = MH2H1 = 45
Угол, вершина которого расположена вне круга, измеряется полуразностью угловых величин дуг окружности этого круга, заключенных внутри угла
угол С = угол BH1A - угол H1AC = 90 - 45 = 45
угол H1AC = половине центрального угла H1MH = 90/2 =45 (вписанный и центральный угол, опирающиеся на одну хорду)
В нашем случае рассматривался остроугольный треуголник, для тупоугольного треугольника - вершина лежит внутри круга, т.е. угол с вершиной внутри круга измеряется полусуммой двух дуг, одна из которых расположена внутри того угла, а другая - внутри угла, вертикального к данному. угол С = 90 + 45 = 135
Ответ: 45 и 135