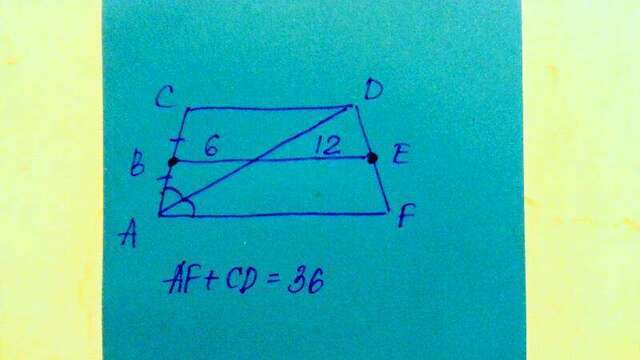В равнобокой трапеции диагональ является биссектрисой острого угла и делит среднюю линию...

Question

В равнобокой трапеции диагональ является биссектрисой острого угла и делит среднюю линию трапеции на отрезки длиной 6 и 12. Найдите периметр трапеции.

Часть решения:
P=a+b+2c
Средняя линия = полусумме оснований
=> сумма оснований = (6+12)*2=36
a+b=36

Теперь нужно найти 2c - равные боковые стороны трапеции

---

Answer 1

Если диагональ трапеции еще и биссектриса, то она отсекает от трапеции равнобедренный треугольник,  боковые стороны которого равны одному из оснований.
Почему - ясно из свойства углов, образующихся при пересечении параллельных прямых секущей. 
Действительно, угол ВСА равен углу САД. Но АС биссектриса, и потому угол ВАС=углу САД, отсюда и угол ВСА равен углу ВАС.
Итак, треугольник АВС - равнобедренный.
Отрезок МО=6, и, т.к. это часть средней линии трапеции, он является средней линией треугольника АВС.
ВС=2 МО=12
АД=2 ОК=24 - на том же основании.
А так как АВ=ВС=СД, то боковые стороны трапеции равны по 12 см. Периметр найдем сложением длин сторон:
Р=2*12+12+24=60

---