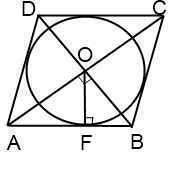
Формула нахождения радиуса вписанной в ромб окружности:
r=(d1*d2)/4a (где d1
и d2 - диагонали ромба, a – сторона ромба)
Построим ромб АВСД со стороной 50 см. и диагональю ВД равной
60 см.
Диагонали ромба пересекаются под прямым углом и точкой
пересечения делятся на равные части. значит ВО=ОД=60/2=30 см.
Зная это по теореме Пифагора найдем отрезок АО
АО=√(АВ^2-BO^2)= √(50^2-30^2)= √(2500 -900)= √1600=40 см.
Вторая диагональ ромба будет равна: АС=АО*2=40*2=80 см.
Найдем радиус вписанной в ромб окружности:
r=(80*60)/(4*50)=4800/200=24
см