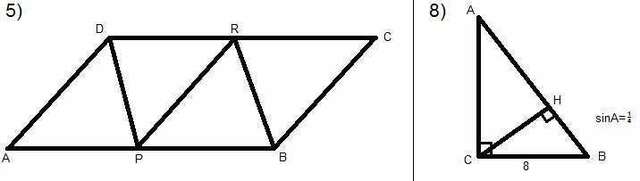
5) пусть R - середина DC
проведем отрезок PR (что-то вроде средней линии параллелограмма), т. к. он проведен через середины сторон параллелограмма, то он разбивает исходный параллелограмм на два равных параллелограмма (AP=PB=DR=RC, AD=PR=BC, AD||PB||BC) с равными площадями.
проведем диагонали DP и RB
рассмотрим треугольники ADP и RDP,
они равны по трем сторонам (AD=PR, AP=DR, DP - общая), а значит их площади так же равны.
Если рассмотреть остальные два треугольника, то можно доказать, что они так же равны.
Т. к. площади параллелограммов ADRP и PRCB равны, то площади всех четырех треугольников равны.
Трапеция DCBP состоит из трех таких треугольников.
Площадь одного треугольника равна 84/4=21,
значит площадь трапеции равна 21*3=63
ответ: 63
8)
по определению синуса
 AB= \frac{CB}{sinA}= \frac{8}{\frac{1}{4}} =8*4=32" alt="sinA= \frac{CB}{AB}=> AB= \frac{CB}{sinA}= \frac{8}{\frac{1}{4}} =8*4=32" align="absmiddle" class="latex-formula">
AB= \frac{CB}{sinA}= \frac{8}{\frac{1}{4}} =8*4=32" alt="sinA= \frac{CB}{AB}=> AB= \frac{CB}{sinA}= \frac{8}{\frac{1}{4}} =8*4=32" align="absmiddle" class="latex-formula">
∠ HCB = ∠ A (в треугольниках ABC и CHB ∠C=∠CHB=90, ∠B - общий)=>
sinA=sin∠HCB=1/4=>
 HB=\frac{CB}{4}=8/4=2" alt=" \frac{HB}{CB}= \frac{1}{4} =>HB=\frac{CB}{4}=8/4=2" align="absmiddle" class="latex-formula">
HB=\frac{CB}{4}=8/4=2" alt=" \frac{HB}{CB}= \frac{1}{4} =>HB=\frac{CB}{4}=8/4=2" align="absmiddle" class="latex-formula">
AH=AB-HB=32-2=30
ответ: 30