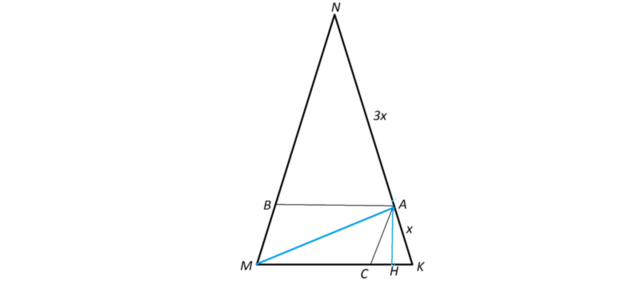
В равнобедренном треугольнике MNK с основанием MK, равным 10 см ,
MN=NK=20 см. На стороне NK лежит точка A так, что AK : AN как 1 : 3. Найти AM.
Сделаем рисунок.
АК
:КN=1
:3
Пусть коэффициент этого отношения будет х.
Так как
NK=20=х+3х=
4x,
AK=20
:4=
5см
Проведем
АВ параллельно основанию МК и АС параллельно боковой стороне NM.
Треугольники MNK и ABN подобны с коэффициентом подобия KN
:AN=4
:3
Cледовательно, МК
:АВ=4
:3
10
:АВ=4
:3
4АВ=30
АВ=
7,5 см
В параллелограмме АВМС противоположные стороны равны.
ВМ=АК=АС=5 см
МС=
7,5 см
Треугольник АСК - равнобедренный.
Найдем по т. Пифагора его высоту АН.
КС=МК-МС=10-7,5=
2,5 см
НК=
1,25 см
АН²= (АК²-НК²)=(5²-1,25²)=
23,4375
Из прямоугольного треугольника НАМ найдем АМ по т.Пифагора
:
АМ=√(МН²+АН²)=√(7,5²+23,4375)=√100=
10 см