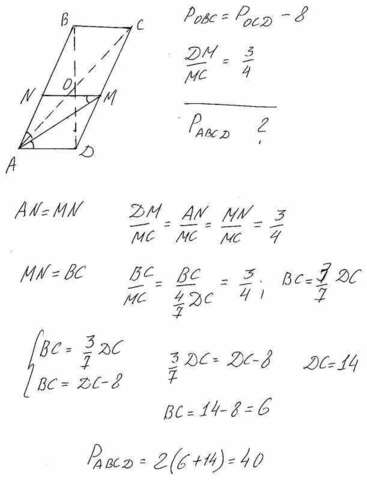
Из точки М проведём прямую параллельно АД(смотри рисунок). Углы ДАМ и NМА равны как накрест лежащие, а углы NАМ и ДАМ-равны по условию, тогда углы NАМ и NМА также равны и треугольник ANM-равнобедренный. Следовательно АN=МN. Поскольку в параллелограмме диагонали в точке пересечения делятся пополам, то периметры треугольников ОВС и ОСД будут состоять из двух равных отрезков ОВ=ОД, общей стороны ОС и сторон ВС и ДС. То есть разность периметров будет равна разности сторон ДС и ВС. Далее, исходя из заданной пропорции находим ДС=14, и ВС=6., а также Равсд=40.