Медиана ВМ треугольника АBC является диаметром окружности,пересекающей сторону ВС в ее...

Question

Медиана ВМ треугольника АBC является диаметром окружности,пересекающей сторону ВС в ее середине.Найдите этот диаметр,если диаметр описанной окружности треугольника АВС равен 12. Совершенно не поняла,даже не знаю,как изобразить это. Помогите,пожалуйста,желательно с чертежом

Answer 1

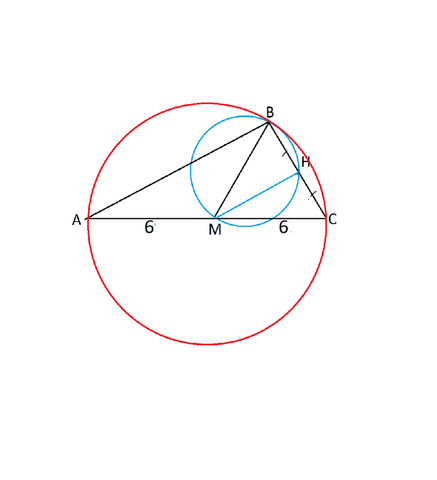
Обозначим точку пересечения окружности и ВС буквой Н. 
ВН=СН. Угол ВНМ опирается на диаметр ВМ, следовательно, он прямой, и МН - высота треугольника ВМС, она же и медиана, т.к. ВН=СН.   ⇒ треугольник ВМС - равнобедренный и ВМ=МС. 
АС - диаметр описанной окружности, а так как точка М - его середина, АМ=МС=6. 
Так как  ВМ - диаметр окружности, пересекающей ВС, и он  равен МС, то он равен 6. 
Ответ:6

---