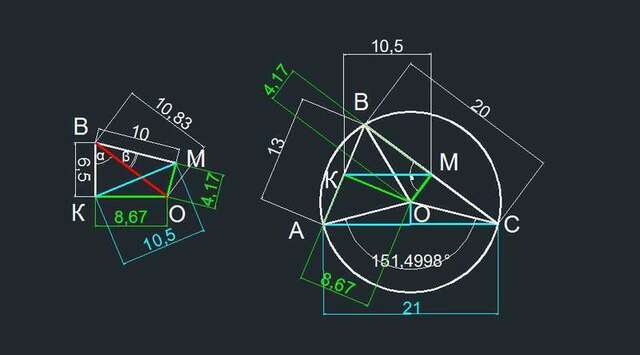
Центр описанной окружности находится на пересечении перпендикуляров к серединам сторон треугольника. Если провести отрезок КМ между серединами известных сторон, то по свойству подобия треугольников он будет равен половине искомой стороны.
Четырехугольник ОКВМ имеет два прямых угла и две диагонали: одна ОВ - это радиус описанной окружности и искомая КМ.
Обозначим углы КВО и ОВМ соответственно α и β.
Стороны ОК и ОМ найдем по Пифагору:
ОК = √(R² - (13/2)²) = √((65/6)²-169/4) = 52/6 = 26/3.
ОМ = √(R² - (20/2)²) = √((65/6)²-100) = √625/36= 25/6.
cos α = (13/2) / (65/6) = 39/65.
cos β = 10 / (65/6) = 12/13.
sin α = (26/3) / (65/6) = 52/65.
sin β = (25/6) / (65/6) = 5/13.
Угол КВО равен α + β.
cos (α+β) = cos α*cos β - sin α*sin β.
cos (α+β) = (39/65)*(12/13) - (52/65)*(5/13) = 16/65.
c = √(a²+b²-2abcos(α+β)).
Для треугольника КВМ а = 6,5 = 13/2, в = 20/2 = 10.
с = √((169/4)+100-2*(13/2)*10*(16/65)) = √(28665/260) =
= √(441/4) = 21/2 = 10,5.
Искомая сторона треугольника равна 2*с = 2*10,5 = 21.