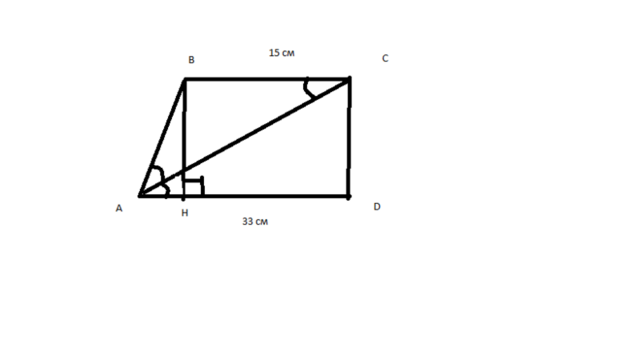
Рисунок во вложениях, там все понятно
Дано: ABCD - трапеция
угол D = 90°
AD - большее основание и равно 33 см
ВС - меньшее основание и равно 15 см
ВН - высота
Решение:
1) Угол CAD = углу ACB, как накрест лежащие углы при параллельных BC и AD и секущей АС⇒
угол ACB = углу CAB.
2) Угол ACB = углу CAB⇒ Δ ABC - равнобедренный
3) Δ ABC - равнобедренный:
AB=BC=15.
4) Найдем высоту трапеции ВН по теореме Пифагора (т.к. Δ АВН - прямоугольный: АНВ=90°):
BH=√(BA ² - AH²) =12
5) Находим площадь:
S=(AD+BC)*BH/2=(15+33)*12/2=288 (см)²
Ответ: 288 (см)²