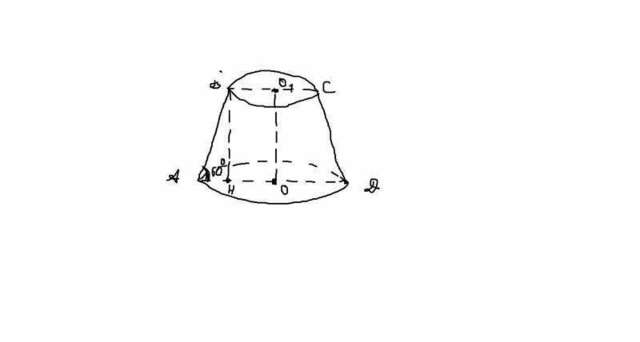
Рисунок уже вот. Сейчас напишу решение, задача нетрудная.
1)Во-первых, как же вычисляется объём усечённого конуса?
V = 1/3 * h(S + S1 +  )
)
Здесь h - высота конуса(задана уже в условии).
S1,S2 - площади обоих оснований конуса.
Видимо, к нахождению этих площадей и сводится эта задача. Теперь уже проще стало рассуждать, когда мы поняли, что нам требуется найти.
2)У нас заданы для чего-то радиусы оснований, точнее, их отношение. Пусть меньший радиус BO1 = x, тогда AO = 2x(больший радиус по условию в два раза больше другого).
Пока нам это ничего не даёт. OO1 - это высота конуса.
3)Из вершины B проведу отрезок BH, ещё одна высота конуса, значит, перпендикулярна плоскости основания. Дан угол между образующей и плоскостью большего основания. Угол между прямой и плоскостью - это угол между прямой и её проекцией на эту плоскость. AH - проекция прямой AB(образующей), значит, 4)А теперь решение понятно. Рассмотрим треугольника ABH, tg 60 = BH/AH = 3 корня из 3 / AH
AH = 3
А теперь легко! AO = 2x, OH = AO - AH = 2x - 3. Заметим, что OH = BO1 = x(как противоположные стороны прямоугольника). Получаем уравнение
2x - 3 = x
x = 3 - это радиус меньшего основания.
Радиус большего в два раза больше, как мы помним, и равен 3 * 2 = 6
5)Теперь легко найти площади оснований.
S1 = 9пи
S2 = 36пи
наша старая формула S = пиr^2 работает.
6)Теперь вычисляем объём. Задача решена.
V = 1/3 * 3 корня из 3 * (9пи + 36пи + 18пи) = 63корня из 3 пи - это ответ.