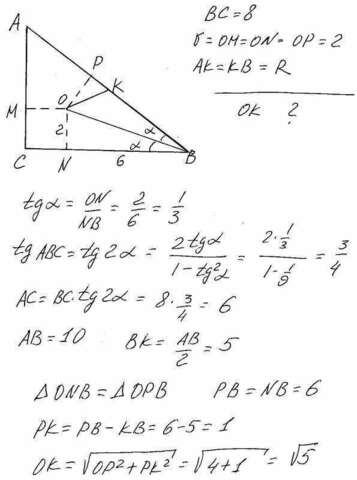
Обозначим треугольник АВС(смотри рисунок). Проведём радиусы ОМ, ОN,ОР. Обозначим точку К-центр описанной окружности, в прямоугольном треугольнике он лежит на середине гипотенузы. Далее NВ=ВС-NC=6. Когда найдём АС-становится ясно, что треугольник -"египетский"(соотношение сторон 3:4:5). Отсюда АВ=10.В дальнейшем исходим из равенства треугольников ONB и OPB (у них гипотенуза ОВ -общая и катеты ON и OP равны как радиусы). Затем по теореме Пифагора. Ответ ОК=корень из 5.