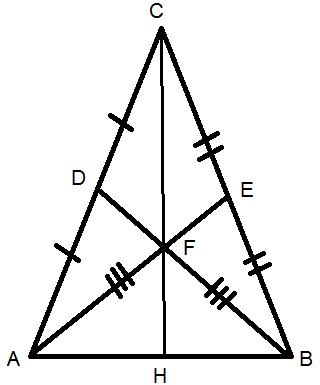
Треугольник на рисунке
точкой пересечения медианы треугольника делят себя на отрезки в отношении 1:2, поэтому если медианы AE и BD равны, то AF=BF. Значит треугольник AFB является равнобедренным, проведем из точки С медиану CH на сторону АВ. Она пересекает две другие медианы в точке F. Т. е. AFB равнобедренный, FH - высота, значит и CH - высота, а медиана является высотой только в равнобедренном треугольнике