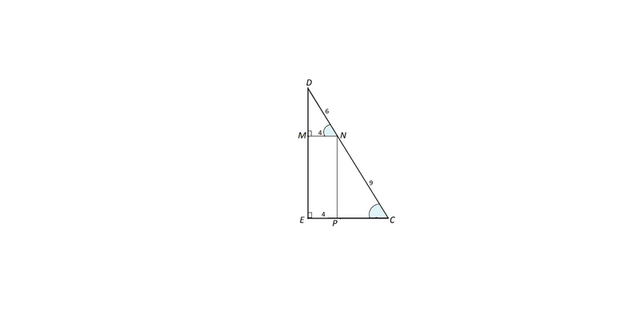
Для решения задачи желательно сделать рисунок.
Гипотенуза СD, следовательно, прямой угол - Е.
Перпендикуляр NР разделил треугольник СЕD на две фигуры:
треугольник NРС и трапецию NРЕD.
Проведя отрезок NМ параллельно СЕ, получим
прямоугольный треугольник DМN и
прямоугольник МNРЕ.
МN=РЕ=4 как стороны прямоугольника МNРЕ.
Треугольники DМN и СЕD подобны.
В них равные углы DNМ и DСЕ по свойству углов при пересечении параллельных прямых МN и СЕ и секущей DС и по прямому углу при М и Е.
Следовательно, косинус ∠С равен косинусу ∠DNМ
cos ∠МND=NM:DN=4/6=2/3
Ответ:cos ∠С=2/3
---------------
Поскольку в условии дана и длина NС, можно удлинить решение, использовав в нём и этот отрезок.
Треугольники DМN и СРN подобны. т.к углы ДNМ и NСР равны по свойству углов при пересечении параллельных МN и СЕ и секущей DС
и по прямому углу при М и Р.
МN:РС=DN:NС
МN=РЕ=4 как стороны прямоугольника МNРЕ.
Отсюда 4:РС=6:9
6 РС=36
РС=36:6=6
Косинусом ∠С является отношение катета РС к гипотенузе NС
или, что то же самое,
cos ∠С=ЕС:DС
cos ∠С=6:9=2/3
Из треугольников DЕС и DNМ получим тот же результат.
cos ∠D=(4+6):(9+6)=10/15=2/3
Ответ:cos ∠С=2/3