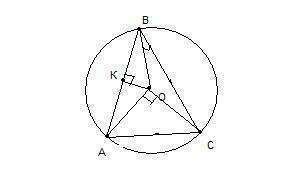
По условию точка О удалена от прямой АВ на 6 см. Расстояние от точки до прямой - длина перпендикуляра от этой точки до прямой, поэтому строим перпендикуляр ОК, равнй 6 см.
Центральный угол АОС опирается на дугу АС, значит градусная мера дуги АС равна 90° также. Вписанный угол АВС опирается на ту же дугу АС и равен ее половине. Значит
Рассмотрим прямоугольный треугольник ОКВ. Гипотенуза ОВ является искомым радиусом окружности. Зная, что катет в прямоугольном треугольнике, лежащий против угла в 30°, равен половине гипотенузы, можем записать:
ОК=ОВ:2, отсюда
ОВ=ОК*2=6*2=12 см