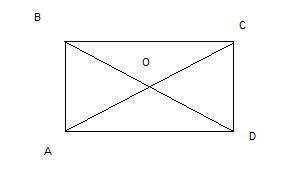
Поскольку прямоугольник является параллелограммом, то он обладает всеми свойствами последнего, и диагонали прямоугольника делятся точкой пересечения пополам. Значит,
АС = АО * 2 = 13 * 2 = 26
По условию АВ : ВС = 5 : 12. Выразим сторону АВ как 5х, а сторону ВС как 12х.
Для прямоугольного треугольника АВС по теореме Пифагора запишем:
АВ² + ВС² = АС²
25х² + 144х² = 26²
169х² = 676
х²= 4
х = 2
Значит АВ = CD = 5*2 = 10, ВС = AD = 12*2 = 24