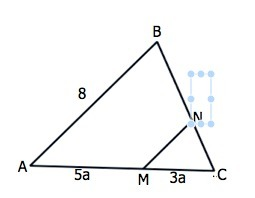
Если прямая параллельна плоскости и содержится в другой плоскости, пересекающей первую, то она параллельна линии пересечения этих плоскостей. ⇒
MN||AB.
Примем коэффициент отношения АМ:МС равным а.
Тогда АС=АМ+МС=8а
∆ АВС ~ ∆ MNC (угол С - общий, соответственные углы при пересечении их параллельных оснований секущими AC и ВС равны)
Из подобия следует отношение:
АС:МС=АВ:MN
8а:3а=8:MN
8MN=24 ⇒
MN=3 (ед. длины)