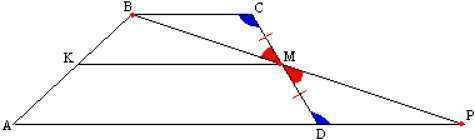
Теорема собственно: средняя линия трапеции параллельна её основаниям, а длина её равна полусумме длин этих оснований.
Доказательство. Дана трапеция АВСD и средняя линия КМ (cм.рис.). Через точки В и М проводим прямую, а сторону AD продолжаем через точку D до пересечения с ВМ. Очевидно, что треугольники ВСМ и МРD равны по стороне и двум углам (СМ = МD, ∠ВСМ = ∠МDР — накрест-лежащие, ∠ВМС = ∠DМР - вертикальные), поэтому ВМ = МР или точка М - середина ВР.
КМ является средней линией в треугольнике АВР. По свойству средней линии треугольника КМ параллельна АР и в частности АD и равна половине АР, что записывается как
КМ = 1\2 AP = 1\2 (AD + DP) = 1\2 (AD + BC), ч.т.д.