Я уже вроде писала...
диаметры относятся так же, как и радиусы...
d/D = (2r) / (2R) = r/R
т.е. нужно доказать, что r/R = a/b
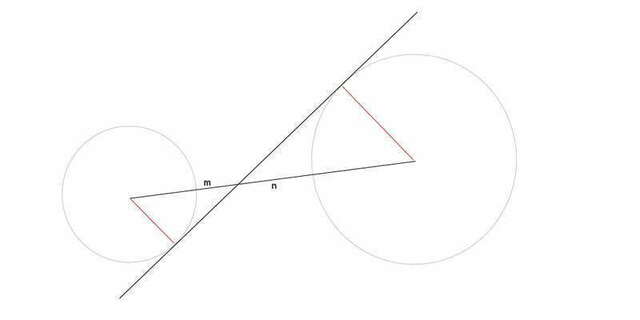
радиусы, проведенные в точку касания _|_ касательной --->
получили два подобных прямоугольных треугольника (в них острые углы вертикальны, т.е. равны...)))
осталось записать отношение соответственных сторон...
гипотенузы относятся как катеты, лежащие против равных (вертикальных)) углов...