Два однакові круги, які дотикаються. Два однакові круги, які дотикаються один одного,...

Question

Дан 1 ответ

Slavka96_zn · Answer 1 · 2018-03-18T20:28:57+0000

Розглянемо рівнобедренний прямокутний трикутник із катетом а. Радіус кола вписаного в нього буде дорівнювати: $r= \frac{2a-a \sqrt{2} }{2}$
Це за формулою для радіуса кола вписаного в прямокутний трикутник: $r= \frac{a+b-c}{2}$
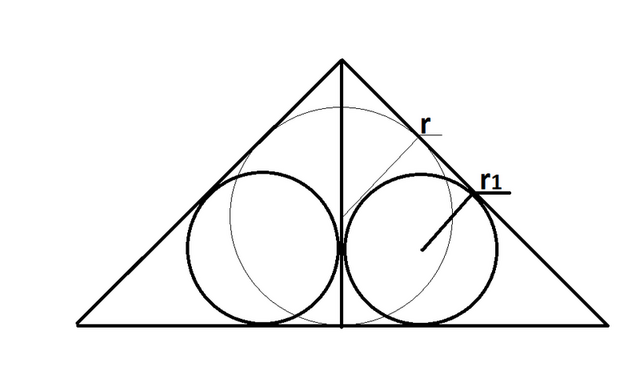
Радіуси менших кіл (див. рис.): $r_1= \frac{a \sqrt{2}-a }{2}$
За умовою задачі площа великого кола вдвічі більша за площу маленького кола, тобто відношення їх радіусів дорівнює $\sqrt{2}$
Знайдемо відношення радіусів відповідних кіл для нашого рівнобедренного прямокутного трикутника, тобто:
$\frac{r}{r_1} = \frac{a(2- \sqrt{2} ) }{2}/ \frac{a( \sqrt{2}-1) }{2} = \sqrt{2}$
Тобто має таку саму величину, як і по умові задачі.
Покажемо, що для іншого виду прямокутних трикутників, крім рівнобедринних, такого відношення між радіусами кіл, що вказані в умові, бути не може. Радіус кола вписаного в прямокутний трикутник обчислюєтсья за формулою:
$r= \frac{s}{p}$ де s= а*в/2 - площа прямокутного трикутника
Цей добуток а*в, як відомо, буде найбільший, коли а=в, тобто катети прямокутного трикутника рівні між собою. Всі інші вписані кола в любі інші прямокутні трикутники, за площею будуть менші від кола вписаного в рівнобедринний прямокутний трикутник, тобто умова задачі в цьому випадку виконуватись не буде. Значить гострі кути цього прямокутного трикутника рівні і дорівнюють 45.
Відповідь: $\alpha = \beta =45^o$